[Java] Binary Tree

과제 (Optional)

- int 값을 가지고 있는 이진 트리를 나타내는 Node 라는 클래스를 정의하세요.

- int value, Node left, right를 가지고 있어야 합니다.

- BinrayTree라는 클래스를 정의하고 주어진 노드를 기준으로 출력하는 bfs(Node node)와 dfs(Node node) 메소드를 구현하세요.

- DFS는 왼쪽, 루트, 오른쪽 순으로 순회하세요.

---

이진 트리란?

트리 구조란? 나무와 비슷한 모양을 가지고 있다고 하여 트리라는 이름이 붙었다.

 

이진트리(Binary tree)는 자식노드가 최대 두 개인 노드들로 구성된 트리를 말한다.

 

이진 트리의 종류는 다양하다. 

- 루트 이진트리 : 하나의 루트 노드를 가지며 모든 노드가 최대 두개의 자식 노드를 가지는 이진트리

- 정 이진트리 : 모든 노드가 0개 혹은 2개의 자식 노드를 가지는 이진트리

- 포화 이진트리 : 모든 내부 노드가 두개의 자식 노드를 가지며, 모든 잎 노드가 동일한 깊이를 가진 이진트리

- 완전 이진트리 : 마지막 깊이를 제외하고 모든 깊이가 완전히 채워져 있는 이진트리

- 균형 이진트리 : 보통 모든 노드의 왼쪽과 오른쪽 하위트리의 깊이 차이가 1이하인 이진트리

 

https://sean-ma.tistory.com/24

 

- 위키 백과 : ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC

 

위키 백과 - 이진트리

 

이진탐색트리의 조건

프로그램 작성에 앞서 이진탐색트리에는 몇 가지 조건이 있다. 조건은 다음과 같다.

1) 이진 탐색트리의 자식 노드 개수는 2개이하이다.

2) 모든 원소는 중복된 값을 가져서는 안된다.

3) 왼쪽 서브트리에 존재하는 노드들의 값은 그 트리의 루트 값보다 반드시 작다.

4)오른쪽 서브트리에 존재하는 노드들의 값은 그 트리의 루트 값보다 반드시 크다.

​

이진탐색트리의 삽입

삽입은 위에서 말한 조건들을 만족시켜 값을 삽입해주면 매우 간단해진다.

​

루트보다 작은 값은 좌측으로 큰 값은 우측으로 빼준다. 이후 서브트리에서도 마찬가지로 조건에 따라 해당 값을 분류해준다. 조건을 맞추다 보면 어느 순간 null값이 나올텐데 그 노드가 바로 해당 값이 들어갈 노드 자리이다.

 

이진탐색트리의 삭제

이진탐색트리의 노드 삭제에는 다음과 같은 세가지 경우가 존재합니다.

​

 

 

세가지 경우는 자신이 삭제하려는 노드가 자식을 몇개 가지고 있는지에 따라 달라지게 된다.

​

1) 자식이 없는경우 : 해당 노드 삭제, 부모 노드의 참조값 삭제.

2) 자식이 1개인경우 : 부모 노드의 값을 자식노드의 값으로 대체해주어야 한다.

3) 자식이 2개인경우 : 자식이 2개인 경우 기 둘 중 하나의 기준을 잡아 노드를 처리해주어야 합니다.

* 삭제하려는 노드의 좌측 최댓값을 삭제노드로 올린다.

* 삭제하려는 노드의 우측 최솟값을 삭제노드로 올린다.

 

 

이진트리 순회

이진트리 순회 방법에는 전위(Pre-order), 중위(In-order), 후위(Post-order) 순회 3가지가 존재한다.

​

*전위순회

전위순회는 루트로 부터 시작하여 왼쪽, 오른쪽을 순차적으로 순회하는 방법을 말한다.

* 중위순회

중위순회는 왼쪽 자식 노드를 방문한 뒤 부모노드, 우측노드를 순서대로 방문하는 구조이다.

* 후위순위

후위순위는 좌측,우측 그리고 부모노드 순으로 순회하는 방식을 말합니다.

 

- 전위 순회 : A -> B -> C -> D -> E -> F -> G

- 중위 순회 : C -> B -> D-> A -> F -> E -> G

- 후위 순회 : C -> D -> B -> F -> G -> E -> A

 

 

 

균형잡힌 이진탐색트리

• 이진탐색트리의 문제점은 무엇일까? 다음의 그림을 보자

 

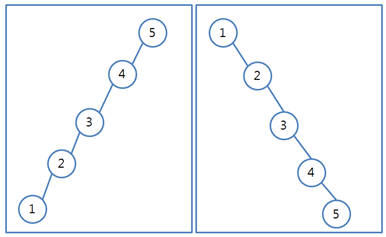
• 다음과 같이 편향된 상태의 이진탐색트리가 계속된다면 데이터의 탐색 수행시간이 O(log n)이 아니라 O(n)에 가까워질 것이다.

• 따라서 편향된 이진탐색트리의 균형을 잡아주는 것이 필요하다.

• 균형잡힌 이진탐색트리의 종류중 가장 유명한 것은 AVL Tree , Red-Black Tree가 있다.

AVL Tree

https://commons.wikimedia.org/wiki/File:AVL_Tree_Example.gif

Red-Black Tree

https://medium.com/@khallilbailey/simple-red-black-trees-b54642bd7652

 

https://medium.com/@khallilbailey/simple-red-black-trees-b54642bd7652

 

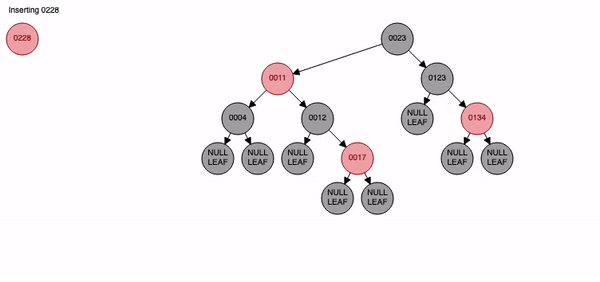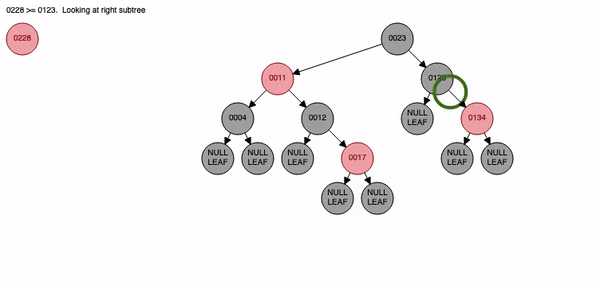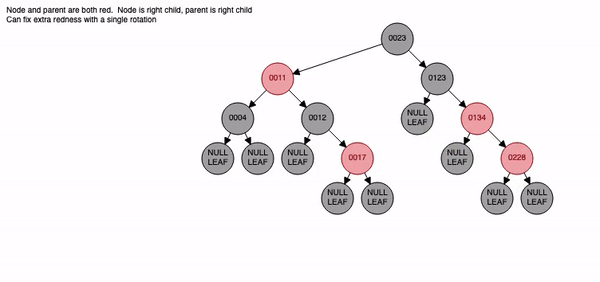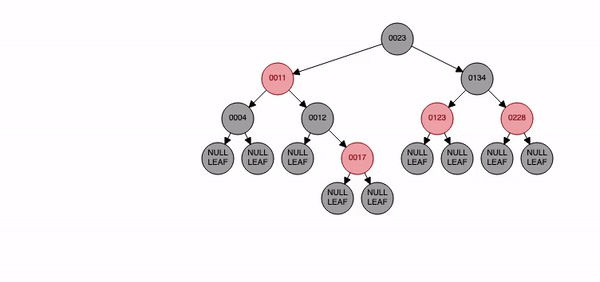
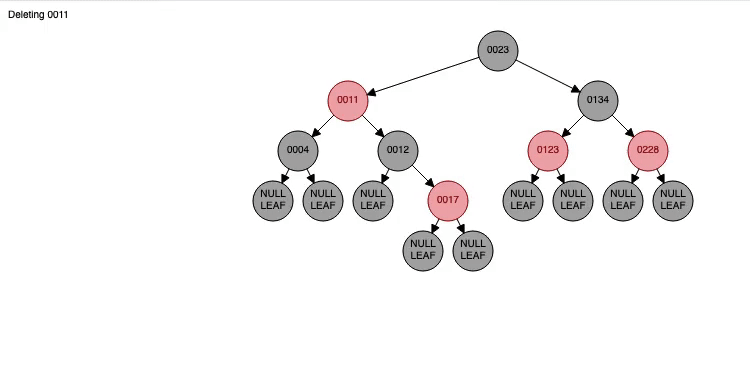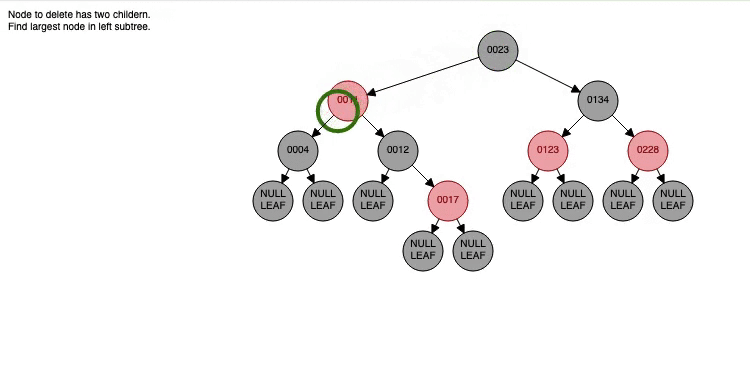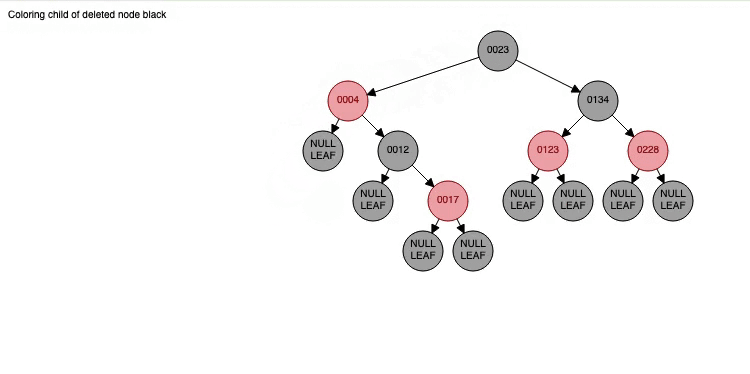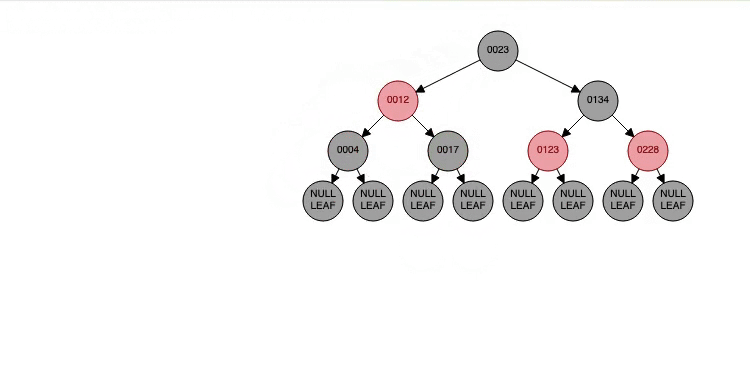
• 위의 방법을 사용하여 균형잡힌 이진탐색트리를 구성면 원하는 데이터를 검색할 때 WorstCase의 시간복잡도를 최소한으로 줄일 수 있다.

• 참고로 자바에서 사용하는 Tree는 Red-Black Tree 기반이다.

힙

• heap 자료구조를 사용하여 자료내에서 최댓값과 최솟값을 빠르게 찾아낼 수 있다.

• 완전 이진트리를 사용한 자료구조이다. 부모노드는 항상 자식 노드보다 우선순위에 있게된다.

https://commons.wikimedia.org/wiki/File:Heap_sort_example.gif

 

 

 

• 자바에서는 다음의 heap자료구조를 PriorityQueue<T> 라는 이름으로 구현해 놓았다.

​